크루스칼 알고리즘은 최소 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘 입니다. 이는 '최소 비용 신장 트리'를 찾는다고 표현하기도 합니다. 사실 구글링을 조금만 해도 설명이 잘된 글이 많아 남들처럼 세세하게 그림을 그리면서 설명하지는 않고, 제가 이해한데로 종합하고자 합니다. 

우선, 알고리즘을 설명하기에 앞서 몇 가지 단어의 개념을 짚고 넘어가고자 합니다. 

간선: 노드끼리 연결한 그래프에서 선에 해당

사이클: 노드끼리 연결한 그래프가 서로 연결되어 루프를 형성하는 경우

여기서 최소 비용 신장 트리에서는 사이클이 발생하면 안됩니다. 간단히 생각하더라도, 사이클이 있으면 거리가 멀어지게 되기 때문에 최소 비용이 아니기 때문입니다. 크루스칼 알고리즘의 순서는 아래처럼 흘러갑니다. 

1. 모든 간선들을 거리를 기준으로 오름차순 정렬 수행

2. 정렬 순서에 맞게 그래프에 포함

3. 포함시키기 전 사이클 테이블을 확인

4. 사이클을 형성하는 경우 간선을 포함하지 않음

- 여기서 사이클 형성 여부를 체크할 때는 Union-Find 알고리즘을 적용

import sys

# Union-Find 와 동일
N = int(sys.stdin.readline().rstrip()) # 노드 수
e = int(sys.stdin.readline().rstrip())
parent = [0] * (N+1) # 부모 행 초기화
# 부모 행 자기자신으로 설정
for n in range(1, N+1):
    parent[n] = n

def find(parent, x):
    if parent[x] == x:
        return x
    parent[x] = find(parent, parent[x])
    return parent[x]

def union(parent, a, b):
    a = find(parent, a)
    b = find(parent, b)
    if a < b:
        parent[b] =a
    else:
        parent[a] = b

# 간선 정보 
edges = []
total_cost = 0

for _ in range(e):
    a, b, cost = map(int, sys.stdin.readline().split())
    edges.append((cost, a, b))
# 거리 기준으로 오름차순 정렬
edges.sort()

for i in range(e):
    cost, a, b = edges[i]
    if (find(parent, a) != find(parent, b)):
        union(parent, a, b)
        total_cost += cost

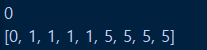
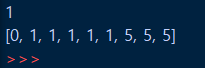
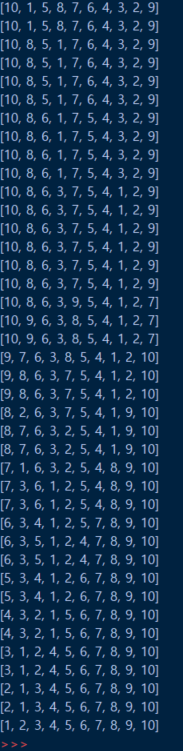
print(total_cost)

입력값을 아래 링크와 동일하게 사진과 같이 넣으면 total_cost가 123으로 동일하게 나오는 것을 확인할 수 있습니다.

참고자료

1. 안경잡이 개발자, "18. 크루스칼 알고리즘(Kruskal Alogrithm)",

https://m.blog.naver.com/PostView.naver?blogId=ndb796&logNo=221230994142&navType=by 

2. Wikipedia, https://ko.wikipedia.org/wiki/%ED%81%AC%EB%9F%AC%EC%8A%A4%EC%BB%AC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

 유니언 파인드(Union Find), 한글로 '합집합 찾기'는 그래프 알고리즘입니다. 알고리즘의 목표는 여러개의 노드에서 선택한 두 노드가 서로 같은 그래프에 속하는지 판별하는 것입니다. 그 과정을 아래 예시를 통해 설명하겠습니다.

 1~8까지 있는 노드를 가정하면, 아래 표와 같이 나타낼 수 있습니다. 위 행은 노드 번호, 아래는 부모노드의 번호로 각 노드가 어떤 부모 노드에 포함되어 있는지를 나타냅니다. 연결이 없이 자기자신만 있는 경우 노드와 부모노드가 같을 것이고, 서로 다른 노드가 연결되는 경우 아래 부모노드가 바뀌게 됩니다.

 1과 2가 연결된 상태를 가정하면, 위표는 아래와 같이 바뀌게 됩니다. 여기서 우리가 세울 규칙은 '연결할 때는 더 작은 값을 부모노드'로 합니다. 여기서 연결은 합침으로도 바꿔 표현할 수 있으며, 그렇기 때문에 Union(합침)이라는 함수가 등장합니다.

 이 상태에서 2와 3을 연결하겠습니다. 위에서 세운 규칙에 따라 3과 연결된 부모노드는 2로 변경됩니다. 하지만, 1과 2가 연결된 상태에서 3도 연결한다면, 1과 3이 연결된 상태인데 이를 나타낼 필요가 있고, 재귀함수를 사용할 수 있습니다. 

 재귀함수는 3의 부모로 2를 찾고, 2의 부모로 1을 찾습니다. 아래와 같이 그림으로 표현이 가능합니다. 이런 과정을 통해 부모 노드를 확인하여 같은 집합에 속하는지 확인하는 것을 Find라고 합니다. 

 즉, Union-Find 알고리즘은 2가지 함수로 구성되며, Union이란 함수를 통해 더 작은 값을 부모노드로 하고, Find라는 함수를 통해 재귀적으로 같은 집합에 속하는지를 확인합니다. 이렇게 확인을 통해 알고리즘의 목표를 달성할 수 있습니다. 그러면 아래 소스코드를 살펴보도록 하겠습니다.

N = int(input()) # 노드 수
parent = [0] * (N+1) # 부모 행 초기화
# 부모 행 자기자신으로 설정
for n in range(1, N+1):
    parent[n] = n

def find(parent, x):
    if parent[x] == x:
        return x
    parent[x] = find(parent, parent[x])
    return parent[x]

def union(parent, a, b):
    a = find(parent, a)
    b = find(parent, b)
    if a < b:
        parent[b] =a
    else:
        parent[a] = b
        
union(parent, 1, 2)
union(parent, 2, 3)
union(parent, 3, 4)
union(parent, 5, 6)
union(parent, 6, 7)
union(parent, 7, 8)

if (find(parent, 1) == find(parent, 5)):
    print(1)
    print(parent)
else:
    print(0)
    print(parent)

노드를 위 사례처럼 8로 입력을 하고 (1,2,3,4)를 연결하고, (5,6,7,8)을 연결했습니다. 

그렇다면, 1과 5를 연결하면 어떨까요? 위 코드 중 union 블록을 아래와 같이 변경하면 결과도 달라집니다.

union(parent, 1, 2)
union(parent, 2, 3)
union(parent, 3, 4)
union(parent, 5, 6)
union(parent, 6, 7)
union(parent, 7, 8)
union(parent, 1, 5)

참고자료

1. 안경잡이 개발자, "17. Union-Find(합집합 찾기)",

https://m.blog.naver.com/PostView.naver?blogId=ndb796&logNo=221230967614&navType=by 

깊이 우선 탐색 (Depth-First Search, DFS)는 저번 BFS에 이은 탐색방법 중 하나로, 표현 그대로 깊이를 우선적으로 탐색하는 알고리즘 입니다. DFS는 맹목적 탐색 방법으로 스택이 사용되며, 여기서 '맹목적 탐색'은 정해진 순서대로 탐색하는 것을 의미합니다. 

알고리즘의 순서는 다음과 같습니다.

1. 스택의 최상단 노드
2. 최상단 노드와 연결된 방문하지 않은 노드가 있으면, 그 노드를 스택에 넣고(push) 방문처리
3. 방문하지 않은 노드가 없으면, 최상단 노드에서 제외
4. 반복 수행

파이썬 코드는 다음과 같습니다.

def depth_first_search(graph, start, visit):
    # 1. 알고리즘 최상단 노드 선택 (방문)
    visit[start] = True
    print(start, end=' ')
    # 현재 노드와 연결된 다른 노드 방문
    for i in graph[start]:
        # 방문하지 않았으면, 재귀적으로 방문처리
        if not visit[i]:
            depth_first_search(graph, i, visit)            
                
graph = [
    [],
    [2, 3],
    [1, 3, 4, 5],
    [1, 2, 6, 7],
    [2, 5],
    [2, 4],
    [3, 7],
    [3,6]
]
visit = [False] * len(graph)
depth_first_search(graph, 1, visit)

구현은 아래 사진처럼 잘 된 것을 확인할 수 있습니다.

위키피디아에서 설며앟고 있는 장단점은 다음과 같습니다.

장점:

- 현 경로상의 노드만 기억하면 되므로 저장공간의 수요가 비교적 적음

- 목표노드가 깊은 단계에 있을수록 해를 빨리 구할 수 있음

단점:

- 해가 없는 경로에 깊이 빠질 가능성

- 최단경로가 아닐 수 있음 

참고자료:

https://m.blog.naver.com/ndb796/221230945092

https://ko.wikipedia.org/wiki/%EA%B9%8A%EC%9D%B4_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89

너비 우선 탐색(Breadth-First Search, BFS)는 이름 그대로, 너비를 우선적으로 하여 탐색하는 알고리즘입니다. 다르게 말하면, 시작점에서 인접한 점을 찾고 방문한 후, 더 이상 방문한 점이 없을 때까지 반복하는 것입니다. 말이 조금 어려운데, 가장 쉽게 이해하자면 기준점에서 가까운 것부터 하나씩 찾아간다고 보시면 됩니다. 

 순서는 다음과 같이 매우 간단합니다.

1. 큐에서 하나의 노드를 꺼냅니다(get)
2. 이 노드와 연결된 노드 중 방문하지 않은 노드를 방문하고, 차례대로 큐에 넣습니다(put)
3. 1-2 반복

파이썬 코드는 다음과 같이 구현할 수 있습니다.

from collections import deque

def breadth_first_search(graph, start, visit):
    queue = deque([start])
    visit[start] = True
    # 큐가 없을때까지 1-2 반복 
    while queue:
        # 1. 큐에서 하나의 노드를 꺼냅니다
        x = queue.popleft()
        print(x, end=' ')
        # 2. 방문하지 않은 노드를 방문하고, 큐에 넣습니다
        for i in graph[x]:
            if not visit[i]:
                queue.append(i)
                visit[i] = True
                
# 아래 블로그 글에 있는 그래프를 구현           
graph = [
    [],
    [2, 3],
    [1, 3, 4, 5],
    [1, 2, 6, 7],
    [2, 5],
    [2, 4],
    [3, 7],
    [3,6]
]
visit = [False] * len(graph)
breadth_first_search(graph, 1, visit)

결과는 아래와 같이 잘 나오는 것을 확인할 수 있습니다.

위키피디아에서 설명하고 있는 BFS의 장단점은 다음과 같습니다.

장점: 출발노드에서 목표노드까지 최단 길이 경로를 보장

단점: 경로가 길 경우 탐색 가지가 증가해 많은 저장소가 필요, 무한그래프나 해가 존재하지 않으면 실패

참고내용:

https://ko.wikipedia.org/wiki/%EB%84%88%EB%B9%84_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89

https://m.blog.naver.com/PostView.naver?blogId=ndb796&logNo=221230944971&navType=by 

지난번 스택에 이어, 자료구조의 또 다른 주요한 형태인 큐(Queue)에 대해 알아보고자 합니다. 스택은 가장 최근 데이터만 끝에서 더해지고 빠지는 일방향의 LIFO 구조라고 했었는데, 큐는 먼저 집어넣은 데이터가 먼저 나오는 FIFO(First-in, First-Out) 구조 입니다. 즉, 양방향이 뚫려 있어 한쪽으로만 데이터가 흐르는 구조라고도 이해할 수 있겠습니다.

큐는 자료를 넣는 put과 자료를 꺼내는 get으로 구분됩니다. 또한, 데이터의 위치에 따라 front, rear로 구분하는데, front는 데이터를 get할 수 있고, rear는 데이터를 put할 수 있습니다. (즉, front는 오래된 데이터, rear는 최근의 데이터가 위치하게 됩니다.)

안타깝게도 파이썬의 리스트를 활용은 원소를 모두 한칸씩 이동시켜야 하는 것 때문에 속도가 느려지게 되고, 그에 따라 큐에 대해서 적합하지 않다고 합니다. 그래도 큐에 대한 구현은 collections라는 것을 통해 가능합니다. 파이썬 공식문서에서 제공하는 예시를 참고하면 다음과 같습니다.

>>> from collections import deque
>>> queue = deque(["Eric", "John", "Michael"])
>>> queue.append("Terry")           # Terry arrives
>>> queue.append("Graham")          # Graham arrives
>>> queue.popleft()                 # The first to arrive now leaves
'Eric'
>>> queue.popleft()                 # The second to arrive now leaves
'John'
>>> queue                           # Remaining queue in order of arrival
deque(['Michael', 'Terry', 'Graham'])

자료구조 중 대표적인 형태로서 스택(Stack)이란 것이 있습니다. 스택은 한쪽 끝에서만 자료를 넣거나 뺄 수 있는 구조로, LIFO(Last-In, First-Out) 형태로 되어 있습니다. 자료를 넣는 것은 push라고 하고, 자료를 빼내는 것은 pop이라고 하는데, 가장 최근 데이터가 입력되고 나오게 됩니다.

파이썬에서는 리스트의 메서드를 활용하면 스택으로 사용하는 것을 쉽게 처리하고 있습니다. 여기서 자료를 넣는 push는 리스트의 append 메서드를 통해, 자료를 꺼내려는 경우 pop을 활용하면 됩니다. 다음은 파이썬 공식문서에서 보여주고 있는 간단한 예시입니다.

>>> stack = [3, 4, 5]
>>> stack.append(6)
>>> stack.append(7)
>>> stack
[3, 4, 5, 6, 7]
>>> stack.pop()
7
>>> stack
[3, 4, 5, 6]
>>> stack.pop()
6
>>> stack.pop()
5
>>> stack
[3, 4]

append를 통해 원소를 넣으면 가장 끝에 데이터가 쌓이고, 아무런 명시적 인덱스가 없는 pop()을 사용하면 데이터가 가장 끝에 있는 데이터부터 빠져나오는 것을 확인할 수 있습니다.

이전에 전세계 발전사업현황에 대한 업데이트에 이어, 국내 발전사업허가 현황을 버블차트로 나타내고자 합니다. 앞서, 게시했던 글에서 문제점 중 하나가 colorbar를 활용해서 편하게 색깔을 표시했지만, 에너지원별로 색의 구분이 쉽지 않았는데요. 이번에는 색에 대한 지정(xkcd)을 통해 좀 더 명확하게 에너지원별로 구분이 될 수 있게끔 하고자 합니다.

우선, 중요한 버전은 다음과 같습니다. Basemap에 대한 설명과 설치에 버전의 영향을 좀 받기 때문에 관련한 내용은 앞서 언급한 전세계 발전사업현황 시각화 글을 참고(링크)하여 주시기 바랍니다.

Version
Python = 3.8.5
numpy = 1.21.3
pandas = 1.1.3
matplotlib = 3.4.3
basemap = 1.2.2

목적은 전기위원회에서 제공하고 있는 발전사업허가 획득 프로젝트들의 현황을 에너지원, 용량, 위치에 대한 정보를 한꺼번에 보여줄 수 있는 시각화를 진행하는 것 입니다. 전반적인 흐름을 간략하게 표현하자면 다음과 같습니다.

1. Basemap을 이용해 한반도 그리기
2. 데이터 확보 및 처리
3. 버블차트 생성

1. Basemap을 이용해 한반도 그리기

우선, 목적한 시각화를 위해 밑그림이 필요합니다. Basemap에는 여러 기능을 제공하고 있는데, 'merc'를 이용해 그려보았습니다. 편의를 위해 draw_hanbando()란 함수를 만들어 Basemap 객체를 관리하도록 했습니다.

%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
import os

os.environ['PROJ_LIB'] = '가상환경 위치'

def draw_hanbando():
    # 한반도 그려내기 
    plt.figure(figsize=(10,10))
    m = Basemap(projection='merc', lat_0=37.35, lon_0=126.58, resolution = 'h',
                urcrnrlat=40, llcrnrlat=33, llcrnrlon=122, urcrnrlon=132)
    m.drawcoastlines()
    m.drawcountries()
    m.drawmapboundary()
    # 위도, 경도를 설정해 한반도가 보이게끔
    parallels = np.arange(30.,50.,1.)
    m.drawparallels(parallels,labels=[True,False,False,False])
    meridians = np.arange(120.,150.,2.)
    m.drawmeridians(meridians,labels=[True,False,False,True])
    return m

m = draw_hanbando()
m

위 코드를 실행하면 아래와 같이 그림이 잘 나오는 걸 확인할 수 있습니다.

2. 데이터 확보 및 처리

다음은 데이터를 확보하고 목적에 부합하게끔 적절하게 처리가 필요합니다. 다행스럽게도(?), 우리나라는 발전사업허가를 취득한 프로젝트들에 대해서 현황대장을 공개하고 있습니다. (링크)를 따라가면 '3MW 초과 발전사업 허가대장'이라는 제목의 공지글을 확인할 수 있는데, 매달 혹은 분기별로 업데이트를 진행하고 있습니다. 아쉬운 점은 불허가 데이터는 없다는 것인데, 이번 글의 목적이 발전사업허가 획득 현황을 보고자함이니 불허건들에 대해서는 다루지 않겠습니다.

위 게시글에 가면, pdf로 된 파일이 있는데 개인적으론 adobe의 힘을 빌어 엑셀로 변환해 사용했습니다. 그리고 데이터를 확인하면, 중복(변경 건) 및 표준화되지 않은 데이터들(용량, 에너지원)이 있는데, 중복은 제거하고 용량 및 에너지원은 약간 노가다로 표준화를 진행했습니다.

이렇게 전처리한 데이터셋을 이용해 14가지의 에너지원으로 분류하여 아래와 같이 정리했습니다. 참고로, 에너지원별로 색에 대한 구분을 확실하게 하기 위해 matplotlib의 color guide에서 이야기하는 색 레퍼런스 중 xkcd를 참조하여 작성했습니다.

# data importing
dataset = pd.read_csv('dataset.csv', encoding='euc-kr') 
# 에너지원별
# color guide: https://matplotlib.org/stable/tutorials/colors/colors.html
groups = dataset.groupby('에너지')
energy = {
    'IGCC':'xkcd:violet',
    'LNG' : 'xkcd:lilac',
    '바이오매스': 'xkcd:taupe',
    '부생가스':'xkcd:lime',
    '석탄': 'xkcd:charcoal grey',
    '수력': 'xkcd:aqua',
    '연료전지':'xkcd:bright pink',
    '열병합':'xkcd:orange',
    '원자력':'xkcd:pale teal',
    '태양광':'xkcd:red',
    '폐기물':'xkcd:eggplant',
    '폐열' : 'xkcd:steel blue',
    '풍력' : 'xkcd:sky blue',
    '해양' : 'xkcd:bright blue'
}

여기서는 언급하지 않았지만, basemap으로 그림을 그리기 위해서는 (x, y) 형태의 좌표가 필요한데요. 아쉽게도, 발전사업허가대장에서는 정확한 좌표를 제공하고 있지 않습니다. 대신 제공하고 있는 주소가 있는데, 이를 이용해 geocoding이 필요합니다. 지오코딩을 위한 방법론은 구글API, ArcGIS 등 다양한게 있지만, 저는 구글을 이용했습니다.

3. 버블차트 생성

과정 1에서 만든 한반도 지도와 과정 2를 통해 얻은 데이터 및 색구분을 활용해 버블차트를 생성할 차례입니다. 위에서 에너지원별로 groupby로 객체를 에너지원별로 나눈 것을 좌표별로 x, y를 대입하고, 크기(s)는 용량/10 (현재 figure size에서 적절한 크기), 색(c)은 에너지원별로 할 수 있게끔 코드를 작성했습니다.

for name, group in groups:
    try:
        # 다른 프로젝트에서 활용한 데이터셋이다보니 여기서는 '불허여부' 존재
        approval = group[group['불허여부']==0] 
        for i in approval.index:
            x, y = m(approval['longitude'][i], approval['latitude'][i])
            m.scatter(x, y, s=approval['용량'][i]/10, c=energy[name],alpha=0.5)
    except:
        continue
plt.show()

위 코드를 실행시켜주면, 아래와 같이 잘 나오는 것을 확인할 수 있었습니다.

참고:

1) 전기위원회 공지사항: https://www.korec.go.kr/notice/selectNoticeList.do

2) 한반도 지도 그리기: wscode, '[Python/Basemap]기상관측망 시각화'

https://wscode.tistory.com/9

[[Python/Basemap]기상관측망 시각화

개발자 D 주제 : Basemap를 활용한 기상관측망 시각화 작업 데이터 : 종관기상관측(ASOS), 방재기상관측(AWS) 기상자료개방포털 ▶ 데이터 ▶ 메타데이터 ▶ 관측지점정보 (data.kma.go.kr/tme

wscode.tistory.com](https://wscode.tistory.com/9)

3) Matplotlib color guide: https://matplotlib.org/stable/tutorials/colors/colors.html

[Specifying Colors — Matplotlib 3.5.0 documentation

Single character shorthand notation for some basic colors. Note The colors green, cyan, magenta, and yellow do not coincide with X11/CSS4 colors. Their particular shades were chosen for better visibility of colored lines against typical backgrounds.

matplotlib.org](https://matplotlib.org/stable/tutorials/colors/colors.html)

4) Basemap 이용: https://seanpark11.tistory.com/64

[[Matplotlib] mpl-toolkits.basemap을 활용한 세계 발전소 데이터를 활용한 발전원별, 용량별 현황시각화

이전에 folium을 활용하여 데이터를 시각화한 적이 있습니다. 하지만, folium을 활용하면 html 형태로 산출물이 나오기 때문에 다른 프로젝트(웹 등) 적용에는 용이하나, 보고서와 같이 A4에 쓰기에는

seanpark11.tistory.com](https://seanpark11.tistory.com/64)

계수정렬은 크기를 기준으로 갯수를 세는 것을 통해 정렬하는 알고리즘입니다. 이전에 했던 정렬 알고리즘과 달리, 비교를 하는 것이 아니기 때문에 위치를 바꿔주는 과정 등이 필요없어 코드가 간결한 편이고, 매우 빠르게( O(n+k) ) 정렬이 가능합니다.

1. array 내 모든 범위를 포함하는 리스트를 만들어 줌. 초기상태는 모든 값이 0인 상태

2. array의 원소를 하나씩 보면서, 해당되는 인덱스의 값(갯수)을 증가시킴

3. 증가된 갯수 리스트에서 0인 값을 제외하고, 인덱스와 인덱스 값(갯수)만큼 출력

비교적 간단한만큼 소스코드도 아래와 같이 간결합니다. array는 기존에 쓰던 것과는 다르게, 이번 정렬의 효과를 좀 더 잘 보여줄 수 있는 것으로 바꿨습니다.

array = [1, 3, 2, 4, 3, 2, 5, 3, 1, 2, 3, 4, 4, 3, 5, 1, 2, 3, 5, 2, 3, 1, 4, 3, 5, 1, 2, 1, 1, 1]

# 계수정렬: 크기를 기준으로 세는 알고리즘
# 범위 조건이 있으면, 빠름
def counting_sort(array):
    count = [0] * (max(array) + 1) # 모든 범위를 포함하는 리스트
    #  각 값에 해당하는 인덱스의 값(개수) 증가
    for i in range(len(array)):
        count[array[i]] += 1
    # 인덱스 출력
    for i in range(len(count)):
        if (count[i] != 0):
            for j in range(len(count)):
                print(i, end=" ")

counting_sort(array)

결과도 아래와 같이 잘 나오는 것을 확인할 수 있습니다.

참고자료:

힙정렬(Heap Sort)은 힙 트리(Heap Tree)를 구성해 정렬하는 방법으로, 앞서 설명했던 병합정렬이나 퀵정렬만큼 빠른 정렬 알고리즘이다. 내림차순 정렬을 위해서는 최대힙을 구성하고 오름차순 정렬을 위해서는 최소힙을 구성해야 한다. 힙을 통해 정렬하는 만큼 힙에 대한 이해가 선행되어야 한다.

힙: 최대값 및 최소값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리의 자료구조

최대힙: 부모노드의 키값이 자식노드의 키값보다 항상 큰 경우

최소힙: 부모노드의 키값이 자식노드의 키값보다 항상 작은 경우

힙생성 알고리즘은 특정 노드의 두 자식 중 더 큰 자식과 자신의 위치를 바꾸는 알고리즘이다. 

array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]

# 1. 상향식: 특정 노드를 기준으로 위로 올라감
def heap_sort(array):
    n = len(array)
    # heap 구성
    for i in range(n):
        c = i
        while c != 0:
            r = (c-1)//2
            if (array[r] < array[c]):
                array[r], array[c] = array[c], array[r]
            c = r
            print(array)
    # 크기를 줄여가면서 heap 구성
    for j in range(n-1, -1, -1):
        array[0] , array[j] = array[j], array[0]
        r = 0
        c = 1
        while c<j:
            c = 2*r +1
            # 자식 중 더 큰 값 찾기
            if (c<j-1) and (array[c] < array[c+1]):
                c += 1
            # 루트보다 자식이 크다면 교환
            if (c<j) and (array[r] < array[c]):
                array[r], array[c] = array[c], array[r]
            r=c
            print(array)
    print(array)
heap_sort(array)

위 코드를 구현하면, 아래와 같이 잘 나오는 것을 확인할 수 있다.

참고자료: