깊이 우선 탐색 (Depth-First Search, DFS)는 저번 BFS에 이은 탐색방법 중 하나로, 표현 그대로 깊이를 우선적으로 탐색하는 알고리즘 입니다. DFS는 맹목적 탐색 방법으로 스택이 사용되며, 여기서 '맹목적 탐색'은 정해진 순서대로 탐색하는 것을 의미합니다. 

알고리즘의 순서는 다음과 같습니다.

1. 스택의 최상단 노드
2. 최상단 노드와 연결된 방문하지 않은 노드가 있으면, 그 노드를 스택에 넣고(push) 방문처리
3. 방문하지 않은 노드가 없으면, 최상단 노드에서 제외
4. 반복 수행

파이썬 코드는 다음과 같습니다.

def depth_first_search(graph, start, visit):
    # 1. 알고리즘 최상단 노드 선택 (방문)
    visit[start] = True
    print(start, end=' ')
    # 현재 노드와 연결된 다른 노드 방문
    for i in graph[start]:
        # 방문하지 않았으면, 재귀적으로 방문처리
        if not visit[i]:
            depth_first_search(graph, i, visit)            
                
graph = [
    [],
    [2, 3],
    [1, 3, 4, 5],
    [1, 2, 6, 7],
    [2, 5],
    [2, 4],
    [3, 7],
    [3,6]
]
visit = [False] * len(graph)
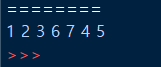
depth_first_search(graph, 1, visit)

구현은 아래 사진처럼 잘 된 것을 확인할 수 있습니다.

위키피디아에서 설며앟고 있는 장단점은 다음과 같습니다.

장점:

- 현 경로상의 노드만 기억하면 되므로 저장공간의 수요가 비교적 적음

- 목표노드가 깊은 단계에 있을수록 해를 빨리 구할 수 있음

단점:

- 해가 없는 경로에 깊이 빠질 가능성

- 최단경로가 아닐 수 있음 

참고자료:

https://m.blog.naver.com/ndb796/221230945092

https://ko.wikipedia.org/wiki/%EA%B9%8A%EC%9D%B4_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89

너비 우선 탐색(Breadth-First Search, BFS)는 이름 그대로, 너비를 우선적으로 하여 탐색하는 알고리즘입니다. 다르게 말하면, 시작점에서 인접한 점을 찾고 방문한 후, 더 이상 방문한 점이 없을 때까지 반복하는 것입니다. 말이 조금 어려운데, 가장 쉽게 이해하자면 기준점에서 가까운 것부터 하나씩 찾아간다고 보시면 됩니다. 

 순서는 다음과 같이 매우 간단합니다.

1. 큐에서 하나의 노드를 꺼냅니다(get)
2. 이 노드와 연결된 노드 중 방문하지 않은 노드를 방문하고, 차례대로 큐에 넣습니다(put)
3. 1-2 반복

파이썬 코드는 다음과 같이 구현할 수 있습니다.

from collections import deque

def breadth_first_search(graph, start, visit):
    queue = deque([start])
    visit[start] = True
    # 큐가 없을때까지 1-2 반복 
    while queue:
        # 1. 큐에서 하나의 노드를 꺼냅니다
        x = queue.popleft()
        print(x, end=' ')
        # 2. 방문하지 않은 노드를 방문하고, 큐에 넣습니다
        for i in graph[x]:
            if not visit[i]:
                queue.append(i)
                visit[i] = True
                
# 아래 블로그 글에 있는 그래프를 구현           
graph = [
    [],
    [2, 3],
    [1, 3, 4, 5],
    [1, 2, 6, 7],
    [2, 5],
    [2, 4],
    [3, 7],
    [3,6]
]
visit = [False] * len(graph)
breadth_first_search(graph, 1, visit)

결과는 아래와 같이 잘 나오는 것을 확인할 수 있습니다.

위키피디아에서 설명하고 있는 BFS의 장단점은 다음과 같습니다.

장점: 출발노드에서 목표노드까지 최단 길이 경로를 보장

단점: 경로가 길 경우 탐색 가지가 증가해 많은 저장소가 필요, 무한그래프나 해가 존재하지 않으면 실패

참고내용:

https://ko.wikipedia.org/wiki/%EB%84%88%EB%B9%84_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89

https://m.blog.naver.com/PostView.naver?blogId=ndb796&logNo=221230944971&navType=by 

지난번 스택에 이어, 자료구조의 또 다른 주요한 형태인 큐(Queue)에 대해 알아보고자 합니다. 스택은 가장 최근 데이터만 끝에서 더해지고 빠지는 일방향의 LIFO 구조라고 했었는데, 큐는 먼저 집어넣은 데이터가 먼저 나오는 FIFO(First-in, First-Out) 구조 입니다. 즉, 양방향이 뚫려 있어 한쪽으로만 데이터가 흐르는 구조라고도 이해할 수 있겠습니다.

큐는 자료를 넣는 put과 자료를 꺼내는 get으로 구분됩니다. 또한, 데이터의 위치에 따라 front, rear로 구분하는데, front는 데이터를 get할 수 있고, rear는 데이터를 put할 수 있습니다. (즉, front는 오래된 데이터, rear는 최근의 데이터가 위치하게 됩니다.)

안타깝게도 파이썬의 리스트를 활용은 원소를 모두 한칸씩 이동시켜야 하는 것 때문에 속도가 느려지게 되고, 그에 따라 큐에 대해서 적합하지 않다고 합니다. 그래도 큐에 대한 구현은 collections라는 것을 통해 가능합니다. 파이썬 공식문서에서 제공하는 예시를 참고하면 다음과 같습니다.

>>> from collections import deque
>>> queue = deque(["Eric", "John", "Michael"])
>>> queue.append("Terry")           # Terry arrives
>>> queue.append("Graham")          # Graham arrives
>>> queue.popleft()                 # The first to arrive now leaves
'Eric'
>>> queue.popleft()                 # The second to arrive now leaves
'John'
>>> queue                           # Remaining queue in order of arrival
deque(['Michael', 'Terry', 'Graham'])

자료구조 중 대표적인 형태로서 스택(Stack)이란 것이 있습니다. 스택은 한쪽 끝에서만 자료를 넣거나 뺄 수 있는 구조로, LIFO(Last-In, First-Out) 형태로 되어 있습니다. 자료를 넣는 것은 push라고 하고, 자료를 빼내는 것은 pop이라고 하는데, 가장 최근 데이터가 입력되고 나오게 됩니다.

파이썬에서는 리스트의 메서드를 활용하면 스택으로 사용하는 것을 쉽게 처리하고 있습니다. 여기서 자료를 넣는 push는 리스트의 append 메서드를 통해, 자료를 꺼내려는 경우 pop을 활용하면 됩니다. 다음은 파이썬 공식문서에서 보여주고 있는 간단한 예시입니다.

>>> stack = [3, 4, 5]
>>> stack.append(6)
>>> stack.append(7)
>>> stack
[3, 4, 5, 6, 7]
>>> stack.pop()
7
>>> stack
[3, 4, 5, 6]
>>> stack.pop()
6
>>> stack.pop()
5
>>> stack
[3, 4]

append를 통해 원소를 넣으면 가장 끝에 데이터가 쌓이고, 아무런 명시적 인덱스가 없는 pop()을 사용하면 데이터가 가장 끝에 있는 데이터부터 빠져나오는 것을 확인할 수 있습니다.

계수정렬은 크기를 기준으로 갯수를 세는 것을 통해 정렬하는 알고리즘입니다. 이전에 했던 정렬 알고리즘과 달리, 비교를 하는 것이 아니기 때문에 위치를 바꿔주는 과정 등이 필요없어 코드가 간결한 편이고, 매우 빠르게( O(n+k) ) 정렬이 가능합니다.

1. array 내 모든 범위를 포함하는 리스트를 만들어 줌. 초기상태는 모든 값이 0인 상태

2. array의 원소를 하나씩 보면서, 해당되는 인덱스의 값(갯수)을 증가시킴

3. 증가된 갯수 리스트에서 0인 값을 제외하고, 인덱스와 인덱스 값(갯수)만큼 출력

비교적 간단한만큼 소스코드도 아래와 같이 간결합니다. array는 기존에 쓰던 것과는 다르게, 이번 정렬의 효과를 좀 더 잘 보여줄 수 있는 것으로 바꿨습니다.

array = [1, 3, 2, 4, 3, 2, 5, 3, 1, 2, 3, 4, 4, 3, 5, 1, 2, 3, 5, 2, 3, 1, 4, 3, 5, 1, 2, 1, 1, 1]

# 계수정렬: 크기를 기준으로 세는 알고리즘
# 범위 조건이 있으면, 빠름
def counting_sort(array):
    count = [0] * (max(array) + 1) # 모든 범위를 포함하는 리스트
    #  각 값에 해당하는 인덱스의 값(개수) 증가
    for i in range(len(array)):
        count[array[i]] += 1
    # 인덱스 출력
    for i in range(len(count)):
        if (count[i] != 0):
            for j in range(len(count)):
                print(i, end=" ")

counting_sort(array)

결과도 아래와 같이 잘 나오는 것을 확인할 수 있습니다.

참고자료:

힙정렬(Heap Sort)은 힙 트리(Heap Tree)를 구성해 정렬하는 방법으로, 앞서 설명했던 병합정렬이나 퀵정렬만큼 빠른 정렬 알고리즘이다. 내림차순 정렬을 위해서는 최대힙을 구성하고 오름차순 정렬을 위해서는 최소힙을 구성해야 한다. 힙을 통해 정렬하는 만큼 힙에 대한 이해가 선행되어야 한다.

힙: 최대값 및 최소값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리의 자료구조

최대힙: 부모노드의 키값이 자식노드의 키값보다 항상 큰 경우

최소힙: 부모노드의 키값이 자식노드의 키값보다 항상 작은 경우

힙생성 알고리즘은 특정 노드의 두 자식 중 더 큰 자식과 자신의 위치를 바꾸는 알고리즘이다. 

array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]

# 1. 상향식: 특정 노드를 기준으로 위로 올라감
def heap_sort(array):
    n = len(array)
    # heap 구성
    for i in range(n):
        c = i
        while c != 0:
            r = (c-1)//2
            if (array[r] < array[c]):
                array[r], array[c] = array[c], array[r]
            c = r
            print(array)
    # 크기를 줄여가면서 heap 구성
    for j in range(n-1, -1, -1):
        array[0] , array[j] = array[j], array[0]
        r = 0
        c = 1
        while c<j:
            c = 2*r +1
            # 자식 중 더 큰 값 찾기
            if (c<j-1) and (array[c] < array[c+1]):
                c += 1
            # 루트보다 자식이 크다면 교환
            if (c<j) and (array[r] < array[c]):
                array[r], array[c] = array[c], array[r]
            r=c
            print(array)
    print(array)
heap_sort(array)

위 코드를 구현하면, 아래와 같이 잘 나오는 것을 확인할 수 있다.

참고자료:

병합정렬, 또는 합병정렬(이후에는 "병합정렬"로 통일)이라고 불리는 merge sort는 O(n * logn) 비교기반 정렬 알고리즘이다. 병합정렬의 기본적인 개념은 다음과 같다.

• 정렬되지 않은 리스트를 원소 1개의 부분리스트로 분할
• 부분리스트가 하나만 남을 때까지 반복 병합하면서 정렬된 부분리스트 생성
• 마지막 하나 남은 부분리스트가 바로 정렬된 리스트

퀵정렬이 빠르고 효율적인 편이라 많은 정렬 알고리즘에 사용한다 했지만, 간혹 특정상황(이미 정렬된 경우)에서는 매우 비효율적이라고 한다. 하지만, 병합정렬의 경우 이러한 특이한 경우가 없이 O(n * logn)의 속도를 보장한다. 병합정렬의 간단한 알고리즘 순서도는 그렇다.

1. 리스트를 절반으로 나눈다. (Divide)
2. 각 리스트를 재귀적으로 병합정렬을 적용해 정렬 (Conquer)
3. 두 리스트를 병합한다. (Combine, Merge)

위 알고리즘에 따라, 참고내용들을 종합해 작성해본 코드는 다음과 같다.

def merge_sort(a):
    def sort(unsorted_list):
        if len(unsorted_list) <= 1:
            return
        # 두개의 리스트로 분할. 아래에서 재귀적으로 시행
        mid = len(unsorted_list) // 2
        left = unsorted_list[:mid]
        right = unsorted_list[mid:]
        merge_sort(left)
        merge_sort(right)
        merge(left, right)
        
    def merge(left, right):
        i = 0
        j = 0
        k = 0
        while (i < len(left)) and (j < len(right)):
            if left[i] < right[j]:
                a[k] = left[i]
                i += 1
                k+= 1
            else:
                a[k] = right[j]
                j += 1
                k+= 1
        # 남은 데이터 삽입
        while i < len(left):
            a[k] = left[i]
            i += 1
            k+= 1
        while j < len(right):
            a[k] = right[j]
            j += 1
            k+= 1
        print(a)
    sort(a)

위 코드를 적용하기 위해 아래처럼 배열을 만들고, 적용해보면 사진처럼 잘 나오는 것을 확인할 수 있다,

array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]
merge_sort(array)

참고자료:

- https://ko.wikipedia.org/wiki/%ED%95%A9%EB%B3%91_%EC%A0%95%EB%A0%AC

- https://m.blog.naver.com/ndb796/221227934987

-

이전까지 기록했던 알고리즘 (선택정렬, 버블정렬, 삽입정렬)들은 시간 복잡도가 O(N**2)로 데이터의 개수가 증가하게 되면, 처리속도가 매우 느려지는 알고리즘들이었다. 하지만, 이번에 구현해보려는 퀵정렬의 경우, 평균적인 복잡도가 O(N*logN)으로 상대적으로 빠른 알고리즘이다. 

퀵정렬의 정의는 다음과 같다. 

" 기준값(pivot)을 기준으로 작거나 같은 값을 지닌 데이터는 앞으로, 큰 값을 지닌 데이터는 뒤로 가도록 하여 분리하며 정렬하는 방법이다 "

정의에서 볼 수 있는 중요 포인트는 1) 기준값이 존재한다는 점, 2) 기준값을 기준으로 분리를 하는 분할정복 알고리즘이라는 것이다. 알고리즘을 이해하고, 상식선에서 같이 알고 넘어가자. 

# 퀵정렬: 특정한 값을 기준으로 큰 숫자와 작은 숫자를 서로 교환한 뒤, 배열을 반으로 나눠 정렬
def partition(arr, start, end):
    pivot = arr[start]
    left = start + 1
    right = end
    done = False
     # left와 right가 엇갈릴 때까지 반복
    while not done:
        # pivot 보다 작은 값을 만날 때까지 반복
        while left <= right and arr[left] <= pivot:
            left += 1
        # pivot 보다 큰 값을 만날 때까지 반복
        while left <= right and pivot <= arr[right]:
            right -= 1
        if right < left:
            done = True
        else: # 엇갈린 상태면 피벗 값과 교체
            arr[left], arr[right] = arr[right], arr[left]
    arr[start], arr[right] = arr[right], arr[start]
    return right

def quick_sort(arr, start, end):
    if start < end:
    	print(arr)
        pivot = partition(arr, start, end)
        quick_sort(arr, start, pivot - 1) # pivot 보다 작은 왼쪽에 적용
        quick_sort(arr, pivot + 1, end) # pivot 보다 큰 오른쪽에 적용
    return arr

quick_sort(array, 0, len(array)-1)

원래 알고리즘에서 코드를 작성할 때는 '안경잡이 개발자' 블로그 및 유튜브를 참고하는데, 이번에는 위키피디아의 소스코드를 참고하였다. 코드 자체는 거의 비슷하고, 구현하는 결과도 거의 비슷했는데, 맨마지막 정렬이 안이뤄져 그에 대한 이유를 아직은 모르겠어서 위키피디아의 내용을 참고했다. 

(원래는 한 함수 내에 모든 것을 끝내려고 했는데, 위키처럼 나눠서 하는 게 나중에 코드에 대한 유지보수의 관점에서 더 쉬울 것이란 생각이다)

순서:

1. pivot 값을 설정한다

2. pivot을 기준으로 보다 큰 값을 만날 때까지(right), 그리고 작은 값을 만날 때까지(left) 비교한다

3. 위에서 찾은 right이 left보다 크면 (값이 엇갈리면) 교체한다

4. pivot 왼쪽과 오른쪽에 위 순서를 반복한다

동작하는 것을 보면 아래 사진과 같이 출력되는 것을 확인할 수 있다. (중복되서 출력되는데, 이건 quick_sort 함수 초반에 print를 하는데, 아래에서는 그 함수를 두번이나 적용하기 때문이다)

참고자료:

- 안경잡이 개발자, "5. 퀵 정렬(Quick Sort)", https://m.blog.naver.com/ndb796/221226813382

- Wikipedia, "Quick Sort(퀵 정렬)", https://ko.wikipedia.org/wiki/%ED%80%B5_%EC%A0%95%EB%A0%AC

삽입정렬은 필요할 때만 적절한 위치에 삽입하는 알고리즘이다. 이것도 시간복잡도는 O(N**2)이나, 필요할 때만 수행하기 때문에 경우에 따라서는 굉장히 빨리 작동할 수도 있다. 따라서 앞서 설명했던 다른 알고리즘들(선택정렬, 버블정렬) 보다는 효율적이라고 할 수 있다. 

삽입정렬의 순서는 다음과 같다고 정리할 수 있다.

1. 주어진 리스트에서 비교할 값을 선정한다

2. 비교할 값을 이전까지의 값들과 '필요한 경우'에만 비교한다

주어진 숫자 리스트를 오름차순으로 정렬하라는 문제에 대하여 위 순서에 따라 코드로 구현해보면 다음과 같다.

# 필요할 때만, 적절한 위치에 삽입하여 정렬
def insertion_sort(array):
    for i in range(len(array)-1):
        j = i
        while (j>=0) and (array[j] > array[j+1]):
            temp = array[j]
            array[j] = array[j+1]
            array[j+1] = temp
            j -= 1
        print(array)
        
array = [1, 10, 5, 8, 7, 6, 4, 3, 2, 9]
insertion_sort(array)

이 알고리즘에서 생각해볼만한 문구는 '필요할 경우에만 비교'한다는 것이다. 일반적으로 어떤 조건에서만 돌아가게끔 하는 반복문은 while을 사용하면 구현이 가능하다는 점을 기억한다면, 앞서 다른 알고리즘에서 for문만 사용하다가 여기서 while문을 만나더라도 당황하지 않을 것이다.

(아래 링크는 파이썬 표준문서에서 이야기하는 while문에 대한 설명이니 필요한 사람만 참고)

https://docs.python.org/ko/3/tutorial/introduction.html#first-steps-towards-programming

다음은 위 코드를 구현했을 때, 정렬 작업의 출력 결과물이다. 상대적으로 이전의 알고리즘에 비해서는 적은 것을 확인할 수 있다.

참고 및 출처:

- 안경잡이 개발자, '4. 삽입정렬(Insertion Sort)' https://blog.naver.com/ndb796/221226806398